Septimius Severus' Ancestors
This is an overview of those ancestors of the emperor Lucius Septimius Severus who were living in Lepcis Magna. The numbers followin the name are based on A.R. Birley, Septimius Severus. The African Emperor (1999³ London), 212-226.
Anno (1)
Only known as father of Gaius from IRT 338.
Gaius (2)
According to IRT 338, this man was the son of Anno and built a portico on the Old Forum in 53/54, which he also paved "in the name of his grandson Gaius Phelyssam". This grandson was the son of Anno Macer, who was the son of Gaius.
Anno Macer (3)
Also mentioned in IRT 338: the son of Gaius and father of Gaius Phelyssam. He adopted a man named Ba'alyaton Commodus, who was responsible for the pavement and colonnade.
Gaius Phelyssam (6)
Mentioned in IRT 338 as the grandson in whose honor Gaius sponsored the paving of the Old Forum and the building of the colonnade. It may be deduced that Gaius Phelyssam had not yet come of age in 53/54, because the responsibility was handed over to his adopted brother, Ba'alyaton Commodus. He appears to have been the father of Septimius Macer.
Ba'alyaton Commodus (4)
Mentioned in IRT 338 as adopted son of Anno Macer, responsible for the building of the colonnade and pavement that Gaius sponsored in honor of Gaius Phelyssam.
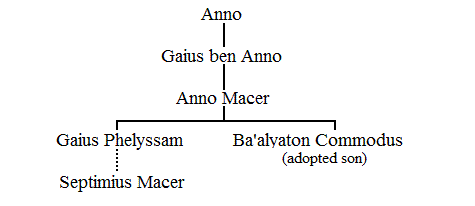
Septimius Macer (23)
Mentioned in the Historia Augusta,note where he is called the emperor's "father's father". This cannot be correct, because we know from IRT 412 that the grandfather of the emperor was Lucius Septimius Severus. The name Macer connects him to Anno Macer and suggests that he was connected to the above-mentioned people; if this is correct, Gaius Phelyssam named his son after his father, a common practice in the ancient world. The name Septimius must have been that of the man who offered Roman citizenship to the family, probably the Septimius Flaccus mentioned by Ptolemy of Alexandria (more...). Whatever his exact connection to the people mentioned above, he is certainly the father of Lucius Septimius Severus and Gaius Claudius Septimius Aper.
Lucius Septimius Severus (26)
Son of Septimius Macer, brother of Gaius Claudius Septimius Aper. He was brought to Italy as a child, and was a friend of the poet Statius, who mentions him twice in the fourth book of his Silvae,note which can be dated to 95. Lucius Septimius Severus owned land near Veii, was a member of the equestrian order, and returned to Lepcis Magna, perhaps after the death of the emperor Domitian in 96. According to IRT 412, Lucius Septimius Severus was suffete, prefect, and one of the two first duovirs of the city, when it was made a colonia during the reign of Trajan (before 110). If we date him between 80 and 140, we cannot be far off the mark. He had a daughter named Septimia Polla and a son named Publius Septimius Geta.
Gaius Claudius Septimius Aper (16)
Gaius Claudius Septimius Aper was a brother of Lucius Septimius Severus. He is known only from IRT 316, a dedication for the health of the emperor Antoninus Pius (r.138-161) and his children. Aper's sons were Publius Septimius Aper and Gaius Septimius Severus, who were both Roman consuls during the reign of Antoninius Pius.
Publius Septimius Aper (15)
The son of Gaius Claudius Septimius Aper, and the first known consul from Lepcis Magna, in 153. As the consulship could not be reached before one had reached the age of 32 years, this man was born in c.120 or earlier. Gaius Septimius Severus was his brother.
Gaius Septimius Severus (25)
This son of Gaius Claudius Septimius Aper and brother of Publius Septimius Aper is best known from the inscription on the Arch of Marcus Aurelius,note erected in 174. It proves that he was proconsul of Africa in that year. Other inscriptionsnote offer further details: he was the son of a Gaius, and had been commander of the Sixteenth Legion Flavia Firmaa, governor of Lycia-Pamphylia, consul in 160, and governor of Germania Inferior. He is probably the "kinsman Septimius Severus, who sought and secured from Marcus Aurelius the senatorial rank" for the future emperor.note
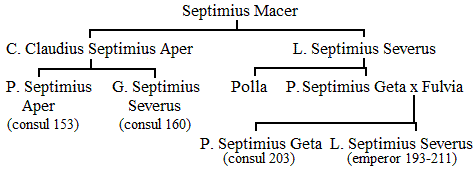
Septimia Polla (10)
Septimia Polla is known from the inscription known as IRT 607, the pedestal of a statue erected by her brother, Publius Septimius Geta.
Publius Septimius Geta (20)
This man was the son of the Lucius Septimius Severus who briefly lived in Italy and became one of Lepcis' two first duovirs, and was the father of the Lucius Septimius Severus who became emperor. According to the Historia Augusta,note he was married to Fulvia Pia, and died when his famous son became quaestor in Baetica (in 171). The Lepcitanians erected an honorific inscription to him,note which mentions no magistracies. He had three children, Publius Septimius Geta, Lucius Septimius Severus (the emperor), and Septimia Octavilla, who was sent away from the imperial court.note
Fulvia Pia (28)
A member of the Lepcitanian Fulvii, an influential family, married to Publius Septimius Geta. She is mentioned in the Historia Augustanote and on IRT 415. Somehow, she was related toGaius Fulvius Plautinianus, the praetorian prefect of Septimius Severus. She gave birth to at least three children, Publius Septimius Geta, Lucius Septimius Severus, and Septimia Octavilla.
Publius Septimius Geta (21)
Son of Publius Septimius Geta and Fulvia Pia, brother of the emperor, mentioned several times in the Historia Augusta, and known from IRT 541, which was erected before 203 because his second consulship is not mentioned. It records his entire career: Xvir stlitibus iudicandis, tribune in the Second Legion Augusta, quaestor for the province Crete and Cyrenaica, aedile of Ceres, curator of the public finances of Ancona, praetor hastarius, tutelarius, commander of the First Legion Italica, governor of Sicily, governor of Lusitania, consul, governor of Moesia Inferior, governor of the Dacian provinces.