Legio XIII Gemina
Legio XIII Gemina: one of the Roman legions. Its surname means "the twin legion".

The Thirteenth Legion was recruited by the Roman general Julius Caesar in 57 BCE, during the war in Gaul, before he attacked the Belgians. He implies the existence of a this unit in his account of the battle against the Nervians, describes how it encountered the Aremoricans and states that it was present during the siege of Gergovia. The blockade of Alesia in 52 must have been among this unit's first operations as well.
During the civil war against Caesar's fellow-triumvir and rival Pompey the Great the men of the thirteenth legion were with Caesar when he crossed the Rubico in January 49.note The Thirteenth was the legion with which, as the historian Livy said, Caesar assailed the world.note
After the conquest of Italy, the legionaries stayed in Apulia for some time. In the winter of 49/48, however, they served at Dyrrhachium. After the decisive battle at Pharsalus, the soldiers were sent back to Italy to be pensioned off (Autumn 48), but in 46, they participated in Caesar's African campaign. They were probably also present during the battle of Munda (45). When Caesar's sole rule was safely established, the legion was disbanded and its veterans were given land at Spello in Italy.

A new Thirteenth Legion is mentioned after 41. This was probably not a new creation but a reconstitution of the old unit. However this may be, it was used by Julius Caesar's heir Octavian, who had to put an end to Sextus Pompeius' occupation of Sicily, which put the grain supply of Rome into peril. On one occasion, soldiers of the Thirteenth saved Octavian's life.
When Pompeius was defeated, Octavian and his fellow-triumvir Mark Antony started a war, which culminated in the naval battle off Actium (31), where Octavian defeated his opponent and won the supremacy in the Mediterranean world. From now on, he was known as the emperor Augustus.
The Thirteenth, which was reinforced with soldiers from disbanded legions and was henceforth known as "the twin legion", was sent to Illyricum or Gallia Transpadana. In c.15, the legion was redeployed in Slovenia, where Augustus' son-in-law Tiberius conquered the Alpine regions. It was now staying at Ljubljana in Pannonia, but the presence of soldiers at Nijmegen in far-away Germania Inferior can be deduced from a graffito on a sherd and an inscription on a helmet.

In 6 CE, Tiberius was to lead at least eight legions (VIII Augusta and XIII Gemina from Pannonia, XV Apollinaris and XX Valeria Victrix from Illyricum, XXI Rapax from Raetia, XIV Gemina and XVI Gallica from Germania Superior and an unknown unit) against king Maroboduus of the Marcomanni in Czechia; at the same time, I Germanica, V Alaudae, XVII, XVIII and XIX were to move against Czechia as well, attacking it along the Elbe. It was to be the most grandiose operation that was ever conducted by a Roman army, but a rebellion in Pannonia obstructed its execution. For three years, the Romans were fighting to restore order on the Balkans, and the Thirteenth was one of the active units.
During the reshuffling of the Roman forces after the battle in the Teutoburg Forest (September 9 CE), the legion was first transferred to Augsburg, maybe briefly to Mainz (with XIV Gemina and XVI Gallica), and finally (in 16?) to Vindonissa (modern Windisch) in Germania Superior, an old Helvetian town. Here, it defended the passes in the Alps against a possible Germanic invasion of Italy. Veterans were settled in Uthina in what is now Tunisia.
During the reign of Claudius (r.41-54), the thirteenth legion was sent to Pannonia, where it stayed at Poetovio, modern Ptuj in Slovenia. This had been the fortress of VIII Augusta, which had now been transferred to the Lower Danube.

During the civil war of 69, XIII Gemina sided with the emperor Otho. (One of its officers was the father of the Roman author Suetonius.) With the First legion Adiutrix, it took part in the battle of Cremona (April), where these units were defeated by V Alaudae, a legion loyal to Otho's rival Vitellius. The new emperor Vitellius, however, did not punish his enemies and merely ordered their return to the Danube after they had helped building a new amphitheater.
In Pannonia, the legion now sided with Vespasian, and was among the victors during the second battle of Cremona (October 69). From here, the Thirteenth was sent to the Rhineland, where the Roman general Petillius Cerialis led an expeditionary force against rebellious Batavians (70).
The emperor Domitian (r.81-96) transferred XIII Gemina to the newly founded fortress at Vindobona (modern Vienna) in 89. The Dacians had invaded the empire in 86 and defeated the legions that were supposed to defend Moesia. In 88, a large Roman army group invaded Dacia and general Tettius defeated its king Decebalus at Tapae; the Thirteenth was one of nine legions involved. Unfortunately, the revolt of the governor of Germania Superior, Lucius Antonius Saturninus, in 89, prevented the ultimate success.
The situation on the Upper Danube was tense as well. XXI Rapax was destroyed. In 92-93, the Thirteenth took part in Domitian's war against the Suebians and Sarmatians.
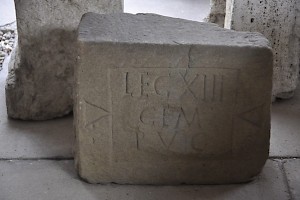
When Dacia had been subjected by Trajan (r.101-106), the Thirteenth stayed behind, probably from the beginning at Apulum (modern Alba Julia). Tiles with the words XIII Gemina and I Adiutrix suggest that it briefly shared its fortress with another legion, but it should be noted that the reading of the tiles is uncertain. Anyhow, I Adiutrix was transferred in c.114.
The Thirteenth was seen as the most important unit in the newly won Dacian territories. It remained there until Dacia was evacuated, although it was often asked to campaign in other provinces. Subunits were sent against the Parthian empire in 115-117 and under Lucius Verus (r.161-169); the presence of a subunit during the war against the Jewish messianic leader Simon ben Kosiba in 132-136 (more) is often assumed.

At the beginning of the reign of Commodus, Pescennius Niger and Clodius Albinus (both future emperors), commanded V Macedonica and XIII Gemina, and defeated the nearby Sarmatians. These two legions were to cooperate often.
In the age of the emperors Commodus to Gordian III (r.180-244), the commanders of the thirteenth legion erected remarkably many altars (no less than seventeen).

In 193, the governor of Pannonia Superior, Lucius Septimius Severus marched on Rome to expel Didius Julianus, who had become emperor after the respected old Publius Helvius Pertinax had been lynched by his soldiers. The Thirteenth sided with Severus, whose reign was to last until 211.
A mixed subunit of XIII Gemina and V Macedonica accompanied Severus to Rome, and later fought for him during his war against his rival, the above-mentioned Pescennius Niger. The soldiers forced the Cilician gate and fought at Issus. It is also possible that they took part in Severus' campaigns against the Parthian empire, which culminated in the sack of Ctesiphon (198).

After the evacuation of Dacia, XIII Gemina was stationed at Ratiaria in Dacia Ripensis (Arçar in northern Bulgaria). Here it still was in the early fifth century. Subunits, usually mixed with soldiers of V Macedonica, are known to have fought against the Alamans during the reign of Claudius II Gothicus (r.268-270) or Aurelian (r.270-275).
Another mixed subunit took part in Diocletian's war in Egypt in 295/296, and was left over there as part of the new garrison of the provincia Herculia, i.e., north-eastern and central Egypt. The legions II Flavia Constantia and III Diocletiana may have similar origins.
Unlike other Caesarian legions, which had the bull as their emblem, the symbol of the Thirteenth, twin legion was a lion. There is no explanation yet.
Literature
- A.S. Hall, "Two Veterans of XIII Gemina at Iconium", in: S. Mitchell (ed.), Armies and Frontiers in Roman and Byzantine Anatolia (1983) 35-40
- J.K. Haalebos, "Römische Truppen in Nijmegen", in: Yann Le Bohec, Les légions de Rome sous le Haut-Empire (2000 Lyon) 465-489
- I. Piso, "Les légions dans la province de Dacie", in: Yann Le Bohec, Les légions de Rome sous le Haut-Empire (2000 Lyon) 205-225
- C. Wolff, "La legio XIII Gemina au Ier siècle", in: Yann Le Bohec, Les légions de Rome sous le Haut-Empire (2000 Lyon) 203-204